Rumus Logaritma dan Fungsinya, Perlu Diketahui
Logaritma adalah kebalikan dari operasi eksponensial.

Logaritma adalah kebalikan dari operasi eksponensial.

Rumus Logaritma dan Fungsinya, Perlu Diketahui
Logaritma adalah kebalikan dari operasi eksponensial. Dalam definisi matematika, logaritma dari bilangan n terhadap sebuah bilangan pokok a adalah eksponen yang harus dipangkatkan pada a untuk menghasilkan n.
Dengan kata lain, logaritma merupakan cara untuk menemukan kekuatan tertentu yang harus dipangkatkan pada bilangan pokok untuk menghasilkan bilangan tertentu.
Cara menulis logaritma adalah dengan menggunakan notasi khusus, yaitu logaritma bilangan n terhadap bilangan pokok a dituliskan sebagai loga(n). Contoh penerapan logaritma adalah dalam penyelesaian persamaan eksponensial, perhitungan pertumbuhan populasi, atau dalam pengukuran tingkat kebisingan atau kecerahan berbagai sinyal dalam sains dan teknologi.
Beberapa sifat-sifat logaritma antara lain: loga(1) = 0, loga(a) = 1, a^loga(n) = n, loga(xy) = loga(x) + loga(y), loga(x/y) = loga(x) - loga(y), dan loga(x^p) = p * loga(x). Sifat-sifat ini memudahkan dalam melakukan operasi-operasi matematika yang melibatkan logaritma.
Berikut rumus logaritma dan contohnya yang merdeka.com lansir dari berbagai sumber:

Rumus Logaritma
Pada bagian sebelumnya kalian telah mengetahui bentuk logaritma. Bentuk logaritma dinyatakan dengan alog b = c.
Simbol a menyatakan bilangan pokok logaritma atau basis, b menyatakan range atau hasil dari logaritma, dan c merupakan domain logaritma.
Persamaan Logaritma
Persamaan logaritma adalah persamaan di mana pengubahnya ada pada bilangan pokok atau numerusnya.
Contoh : (i) log (3x – 1) = log (x – 15) , (ii) (x-1)log 16 = 2, dll.
Macam-macam bentuk persamaan logaritma :
1. alog f(x) = alog p f(x)log a = g(x)log a2. alog f(x) = alog g(x) f(x)log g(x) = f(x)log h(x)3. alog f(x) = blog f(x) A.(a log x)2 + B(a log x) + C = 04. f(x)log g(x) = p untuk A ¹ 0
Bentuk persamaan logaritma pada umumnya masih belum sederhana. Oleh karena itu, untuk membuat persamaan logaritma menjadi lebih sederhana, perlu memperhatikan sifat-sifat logaritma berikut :

Dalam menyelesaikan persamaan logaritma, kita perlu menyamakan bilangan pokok logaritmanya terlebih dulu. Nilai penyelesaian yang diperoleh perlu diuji dengan dengan cara mensubstitusikan ke persamaan semula. Nilai penyelesaian yang menjadi anggota himpunan penyelesaian (HP) adalah yang mengakibatkan:
Numerus pada persamaan semula bernilai bilangan pokok logaritma pada persamaan semula bernilai positif dan tidak sama dengan 1 (satu).
Sifat Logaritma
Berikut sifat logaritma:
ª log a = 1ª log 1 = 0ª log aⁿ = nª log bⁿ = n • ª log bª log b • c = ª log b + ª log cª log b/c = ª log b – ª log cªˆⁿ log b m = m/n • ª log bª log b = 1 ÷ b log aª log b • b log c • c log d = ª log dª log b = c log b ÷ c log a
Fungsi Logaritma
Fungsi Logaritma adalah fungsi invers (kebalikan) dari fungsi eksponen. Jadi, jika fungsi eksponen dinyatakan dengan f(x) = ax, a > 0, a ≠ 1, maka invers dari f(x0 ditulis dengan f-1(x) = alog x atau f(x) = alog x, a > 0, a ≠ 1.
Secara umum bila y = ax, maka x = alog y.
Bila f(x) = alog x, dengan a > 1, x > 0 , x e R, maka f(x) dikatakan fungsi Bila f(x) = alog x, dengan 0 0 , x e R, maka f(x) dikatakan fungsi naik.
Grafik fungsi logaritma selalu melalui titik (1,0) dan selalu berada di sebelah kanan sumbu Y.
Untuk lebih jelasnya, Anda bisa memperhatikan gambar di bawah ini:
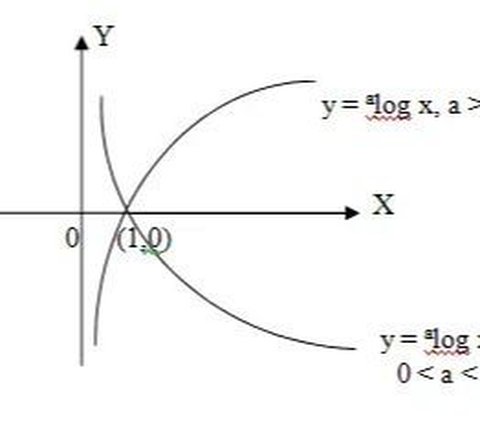
Dari grafik fungsi logaritma di atas, dapat terlihat bahwa:
Untuk a > 1
Bila alog f(x) ³ alog g(x), maka f(x) ³ g(x), dengan syarat f(x) dan g(x) > Bila alog f(x) £ alog g(x), maka f(x) £ g(x), dengan syarat f(x) dan g(x) >
Contoh Soal dan Jawaban
Berapa nilai dari 2log 4 + 2log 12 – 2log 6 = ?
Pembahasan :
Untuk menjawab soal seperti di atas, Anda perlu mengingat sifat logaritma
alog(b.c) = alog b + alog c, dan alog = alog b – alog c
Jadi, untuk menyelesaikannya, kita akan menggunakan kedua sifat logaritma tersebut, sehingga perhitungannya menjadi :
2log 4 + 2log 12 – 2log 6 = 2log
= 2log 8
Kemudian, untuk penyelesaian akhir, kita perlu mengingat sifat berikutnya, yaitu :
alog = n . alog b
→ 8 =
sehingga, penyelesaian akhirnya akan menjadi:
2log 8 = 2log
= 3 . 2log 2 → jangan lupa dengan yang ini : alog a = 1
= 3 . 1
= 3
Perkalian dan pembagian logaritma
Sifat perkalian logaritma menyatakan bahwa logaritma dari hasil perkalian dua bilangan sama dengan penjumlahan logaritma masing-masing bilangan. Dengan kata lain, log (ab) = log(a) + log(b). Contohnya, jika log(2) = 0.3010 dan log(5) = 0.6990, maka log(10) = log(2 x 5) = log(2) + log(5) = 0.3010 + 0.6990 = 1.
Sedangkan untuk pembagian logaritma, sifatnya mengatakan bahwa logaritma dari hasil pembagian dua bilangan sama dengan selisih logaritma masing-masing bilangan. Artinya, log(a/b) = log(a) - log(b). Misalnya, jika log(8) = 0.9031 dan log(2) = 0.3010, maka log(4) = log(8 / 2) = log(8) - log(2) = 0.9031 - 0.3010 = 0.6021.
Perlu diperhatikan bahwa perkalian logaritma dan logaritma perkalian adalah dua konsep yang berbeda. Perkalian logaritma mengacu pada sifat perkalian logaritma (log(ab) = log(a) + log(b)), sedangkan logaritma perkalian mengacu pada logaritma dari hasil perkalian dua bilangan.