Standar Deviasi adalah Rumus Statistika, Ketahui Cara Menghitung dan Kegunaannya

Merdeka.com - Standar deviasi adalah sebuah rumus yang sering digunakan dalam bidang ilmu statistika. Rumus yang diperkenalkan oleh Karl Pearson pada 1894 ini, juga biasa digunakan untuk melihat sebaran statistik secara lazim. Dengan rumus ini, kita bisa mencari rata-rata jarak penyimpangan pada data yang telah didapatkan.

Melansir dari Investopedia, standar deviasi adalah nilai statistika yang digunakan untuk menentukan bagaimana persebaran data dalam suatu sampel dan melihat seberapa dekat data-data tersebut dengan mean atau rata-rata dari sampel tersebut. Sederhananya, rumus yang biasa disebut dengan simpangan baku ini berfungsi untuk menentukan seberapa heterogen elemen data yang ada dalam sebuah data.

Lantas, apa sebenarnya standar deviasi dan bagaimana cara menghitungnya? Simak ulasannya yang merdeka.com lansir dari Investopedia:

Mengenal Rumus Standar Deviasi

biofar.id

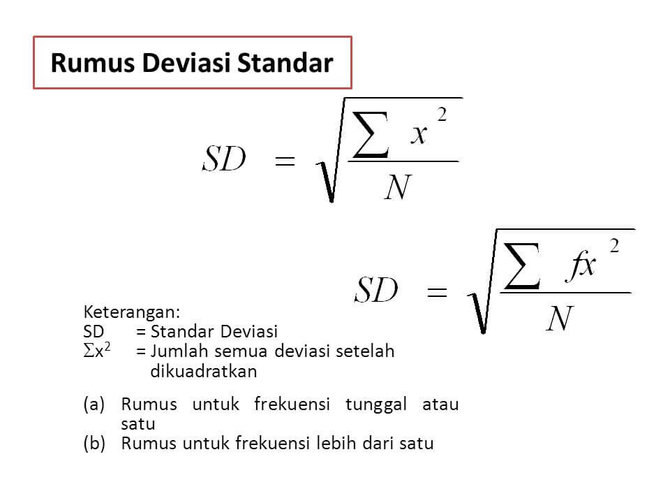
Standar deviasi adalah rumus dalam statistika yang dapat digunakan untuk mendapatkan data dari suatu populasi. Standar deviasi atau yang biasa disebut simpangan baku ini disimbolkan dengan alfabet Yunani sigma σ atau huruf latin S.

Dalam pembentukan rumus standar deviasi didasarkan pada rumus variansi. Sebab, standar deviasi adalah akar kuadrat dari variansi. Dalam mencari variansi, selisih dari tiap elemen data dengan mean data dihitung.

Dalam rumus ini, variansi dibagi menjadi dua, yaitu variansi sampel (S2) dan variansi populer (σ2). Hal ini juga berlaku dalam standar deviasi, yang merupakan akar kuadrat variansi. Sehingga, standar deviasi juga turut dibedakan menjadi dua, standar deviasi sampel (S) dan standar deviasi populasi (o).

Cara Menghitung Standar Deviasi

sxc.hu

Cara menghitung standar deviasi bisa dibedakan menjadi dua, yakni menghitung standar deviasi data individu dan data kelompok. Baik data individu maupun data kelompok, cara menghitungnya adalah mencari nilai rata-rata atau mean, setelah itu dilanjutkan dengan menghitung selisih setiap data dengan nilai rata-rata, dan memasukkan data-data yang ada ke dalam rumus deviasi.

Cara Menghitung Standar Deviasi dengan Kalkulator

Cara menghitung standar deviasi juga bisa dilakukan dengan kalkulator. Tentu saja, kalkulator yang bisa digunakan adalah kalkulator sains. Berikut cara menghitung standar deviasi menggunakan alat bantu kalkulator:

1. Langkah pertama, buka kalkulator dan klik tombol Mode yang ada di ujung kanan atas.

2. Setelah itu, pilih mode statistik dan tekan tombol nomor 1 (VAR-1).

3. Masukkan data yang ingin dihitung dengan cara memasukkan angka, tekan tombol sama dengan, masukkan angka lagi, dan begitu seterusnya.

4. Tekan tombol AC.

5. Setelah itu, tekan tombol SHIFT.

6. Untuk mengetahui hasil akhir, tekan tombol 1 (STAT), 4 (VAR), (σ x). Kemudian tekan tombol sama dengan.

Kegunaan Standar Deviasi

sxc.hu

Standar deviasi adalah sebuah rumus yang kerap dimanfaatkan para ahli statistika untuk mengetahui apakah sampel data bisa mewakili seluruh populasi. Ada banyak kegunaan standar deviasi, seperti memberikan gambaran tentang persebaran data terhadap data rata-rata. Dengan standar deviasi, seseorang bisa memberi gambaran kualitas data sampel yang diperolehnya.

Tak hanya itu, standar deviasi juga dapat memberikan gambaran nilai ketidakpastian saat melakukan pengukuran berulang. Sehingga, rumus ini bisa mempermudah seseorang ketika melakukan sebuah penelitian. (mdk/jen)